If you’ve been to a hackathon recently, you might have noticed a suspicious uptick in the amount of compression related projects. Seriously, they’re everywhere, and it’s no mystery why. One of the things that makes Silicon Valley great is that—tequila-powered keyboards aside—everything on the show is so accurate, from the personalities down to the actual tech involved.
What’s compression in the first place? At its most basic, compression is a way of representing data using less space. An emoji is a good metaphor: it represents an entire word or even several words using a single character. Our minds then “decompress” the character back into the word it represents.
When hackers see a magical plot-driving compression algorithm, it’s hard to chalk it up as simply a narrative device. After all, universal lossless compression sounds pretty sweet. So, at a recent hackathon, I decided to get to the bottom of middle-out compression.
First, a shout out to the good folks at Kayak for indulging me at their hackathon in my attempt to reverse-engineer the Pied Piper compression engine. If you’re in Boston the next time it’s held, you should check it out! Also, sorry for the manic scribbles all over your brand new windows.
What makes Pied Piper special anyway?
Let’s start with what makes Pied Piper special in the first place: that magical 5.2 Weissman compression score. The origin of the Weissman score is actually one of my favorite parts about the show. Essentially, the writers were having a hard time coming up with a compression ratings system that viewers would understand. So, they asked Stanford engineers to make one up.
They came back with a simple metric that—in a plot twist worthy of Mike Judge—is now being adopted in the real world.
Scary math aside, the equation means that any compression algorithm tested is ranked against a known one, like ZIP or TAR. But that’s essentially all we’re given. And this is where our problem begins. Silicon Valley is full of details designed to be technically accurate, but so vague that nerds like me can’t stop picking everything apart. So, what can we infer from the available information? Fortunately, there are plenty of clues.
Clues from the Show
In the Season 1 finale, Richard brags that his algorithm can “view the whole file at once”, rather than piece by piece. He specifically contrasts Pied Piper with 3 types of encoding:
- Shannon Encoding – One of the earliest compression algorithms, Shannon coding essentially just sorts the elements of a file from most to least likely to appear.
- Huffman Encoding – This approach creates a binary tree based on how often each element of a file appears, allowing us to decompress by simply walking the tree.
- Lempel-Ziv-Welch Encoding – LZW coding reads the file letter by letter and dynamically builds a dictionary of the most commonly used strings. Decompression is as easy as search-and-replace.
Shannon coding was nowhere near as good as Huffman in most cases (it predates it), so we can comfortably ignore that one. The details behind Huffman and LZW encoding are fairly in the weeds, but a feature common to both is that they go through a given file and build up a structure that’s used for decompression. Since Richard explicitly states at TechCrunch Disrupt that Pied Piper follows a different approach, we can rule both of these out. So what’s left?
In Season 2, Richard diagrams Pied Piper for the End|Frame engineering team, but after reviewing the whiteboard scene frame by frame, I’ve concluded that the only details that appear pertain to the ingestion engine–the code that provides a better environment for the algorithm to run in, not the actual compression algorithm itself.
In the second episode of Season 2, Gilfoyle provides us with a possible solution. He mentions a “probabilistic model,” suggesting that the algorithm uses elements of chance to work properly.
So to recap, we have two pieces of information to go off of:
- The algorithm does not build any complex decompression.
- The algorithm incorporates some element of luck.
My Sample Solution
After several cans of Red Bull and a lot of frantic pacing, I arrived at a version of middle-out that satisfies both of the above requirements: Pied Piper doesn’t build anything; rather it has a fixed dictionary as a single long file containing the most statistically likely bit patterns. This satisfies both requirements.
Next, it goes straight through the file and scans chunks indiscriminately for bit patterns. If a “chunk” exists in the likely file, we store that chunk’s location in the likely file in the output file.
Chunk: 1011
Likely file: 0101100011001
1011
||||
0101100011001
So here, for example, we just write the number “1” instead of the chunk because the pattern can be found at index 1 of the likely file. Now, obviously there are some chunks that are not found in the likely file. When that happens, we need to encode the changes needed to make the data from the likely file match the data in the chunk. Observe:
Chunk: 1011
Likely file: 0101100011001
1111
|X||
0101100011001
In this case, we still put “1” in the output file, because the index is the same, but we also encode the locations where we need to “flip” a bit from 0 to 1 or vice versa to rebuild the original chunk.
The Big Problem (and solution)
“Wait!” you might say. If the chunk is 4 bits long, and we’re using a 4-bit int as the index, that means we actually start losing efficiency as soon as we have to alter a single bit! Basically, any time we need to deviate from the most statistically likely patterns, we actually make the files bigger!
Don’t believe me? Take a look!
At this point, I started banging my head against my desk because running into a problem like this at four in the morning is enough to make you cry. But then, while I was halfheartedly re-testing scripts and wondering how long it would take to accomplish something vaguely useful, I had a breakthrough! What if we used the ability to create custom data types and changed the size of the index variable based on chunk size?
For example, a 4-bit chunk has addresses 0-3, all of which can be represented by only 2 bits. This allows us to specify 2 addresses before we have a net loss of efficiency. Likewise, an 8-bit chunk would only require a 3-bit address, allowing us to store 3 before going into the red. Small chunks don’t need as many flips; perfect or near perfect matches are more likely to appear. Big chunks need more bitflips since they’re less likely to have near or perfect matches, but as a result can have more bitflips while still preserving efficiency.
It gets better. Look what happens when we write it out!
Look at the amount of possible bitflips! With a system like this, they accelerate with chunk size! Theoretically, this means that the algorithm gets more efficient as it scales up with larger and larger files. This means that there’s a minimum size for effective compression, but if we were using binary searching to find the addresses in the likely file, a middle-out compression algorithm wouldn’t take much longer to compress a 1080p movie than a text file. Neat, huh?
Lack of Hits
At this point, I was dancing around, somehow thinking I had done what Knuth couldn’t and magically devised compression in constant time. Since I’m not receiving a Nobel Prize, or getting sued by Hooli, this obviously isn’t the case.
My stumbling block seemed to be that, no matter what I tried, there were uncharacteristically few matches or near matches. No likely file of any quickly searchable size can contain enough patterns for the entropy of a large file. And it turns out that one of our old friends from Hooli can help us solve the mystery as to why.
While the information behind him isn’t of much value to us, (test results for different waveforms) the Hooli brogrammer does mention DCT (Discrete Cosine Transformation), filter banks and DFT (Discrete Fourier Transformation) butterflies, common in blocked encoding schema. Richard must therefore be solving the hit problem by implementing some kind of blocked compression before using “middle-out” analysis.
My guess would be that Richard is using LZ4 compression, the lightning fast blocked compression algorithm used in everything from Linux and BSD kernels to Battlefield 4 and Hadoop. This algorithm significantly lowers randomness and increases the likelihood of a match/near match. Furthermore, it’s fast enough to not make a huge difference in algorithm speed, and adds regularity.
Tests
Conjecture is well and good, but we want to see if middle-out compression actually works. So, I threw some sample files together and through the power of some hideous bash and C scripts, I was able to get some results! The algorithm works much better with complex video files as illustrated in the examples below. (Also of note. Why do the top image searches for these two shows look so similar?)
The disheartening conclusion: Richard’s magical compression performed no better than existing compression schemes, and in some cases performed worse. While bit-shifting on its own is phenomenal for compressing certain kinds of updates, and probabilistic models are great for sorting and mathematics, neither of them seem to pose particularly great promise for universal compression.
In any case, thanks for reading. Please let me know if I overlooked anything that could make me a member of the Three Comma Club. I want a boat. And doors that open vertically.
Alex Gould is a low level systems programmer and C fanboy. He’s been to more than 10 hackathons and will be attending Hack the Planet in August. He’s also addicted to kimchi.

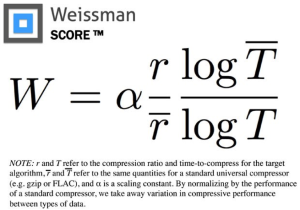



tar is not a compresion algorithm https://en.wikipedia.org/wiki/Tar_(computing) but there’s a possibility to use tar and then compress with something else..
What aboud cloud compression where you use deep learning to continuously develop your unique-block library.